Mathematik-
Vertiefungskurs
Dietrich-Bonhoeffer-Gymnasium
Albrecht-Dürer-Straße 9-11
90522 Oberasbach
Telefon: (0911) 69 98 2-0
Fax: (0911) 69 98 2-49
Auf dieser Seite findet sich ein Überblick über die im Mathe-Vertiefungskurs behandelten Inhalte.
Im Lehrplan für den Mathe-Vertiefungskurs (PDF-Datei, ca. 57 kB) sind fünf Module aufgeführt. Die Lehrkraft des Mathe-Vertiefungskurses wählt - ggf. auch in Absprache mit den Kurs-TeilnehmerInnen - drei der fünf Module aus, die in den Halbjahren 12/1 und 12/2 behandelt werden.
Wir blicken zurück auf die Erweiterungen der Zahlenbereiche, die wir beim bisherigen Mathematik-Lernen kennengelernt haben:
Von den natürlichen Zahlen ℕ über die ganzen Zahlen ℤ und die rationalen Zahlen ℚ bis zu den reellen Zahlen ℝ. Damit konnten für immer neue Gleichungen Lösungen gefunden werden.
Doch auch in der Menge der reellen Zahlen haben manche Gleichungen, z. B. die Gleichung x2 + 1 = 0, keine Lösung. Wir lernen, dass deshalb die imaginäre Einheit "i" eingeführt wurde, für die i2 = -1 gilt, woraus sich komplexe Zahlen der Form z = a + bi ergeben.
Komplexe Zahlen können aus den reellen Zahlen konstruiert werden, nämlich als Paare (a; b) reeller Zahlen a und b. Zum besseren Verständnis stellen wir komplexe Zahlen in der Gaußschen Zahlenebene ℂ dar, also nicht wie die reellen Zahlen auf nur einer Zahlengeraden.
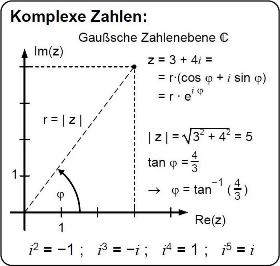Wir lernen, wie man mit komplexen Zahlen in der Summenform z = a + bi rechnet. Das Multiplizieren und Dividieren, noch mehr das Potenzieren und Radizieren komplexer Zahlen in Summenform stellt sich dabei als schwierig heraus. Einfacher ist dies bei komplexen Zahlen in Polarform z = r ‧ E(φ), wobei E(φ) = cos φ + i sin φ ist.
Wir gewinnen ein Verständnis dafür, dass eine Gleichung n-ten Grades in der Menge der komplexen Zahlen stets n Lösungen hat (nicht notwendigerweise verschieden), anders als in der Menge der reellen Zahlen, bei denen eine quadratische Gleichung (Gleichung zweiten Grades) zwei, eine oder auch keine Lösung haben kann.
Die Menge der komplexen Zahlen ℂ ist also algebraisch "leistungsfähiger", zudem ein Körper (algebraische Struktur). Jedoch gibt es in ℂ keine Ordnungsrelation ("kleiner als"), man kann also von zwei komplexen Zahlen z1 und z2 nicht sagen, welche die kleinere bzw. größere ist.
Wir lernen, dass eine Folge eine Abbildung von der Menge der natürlichen Zahlen in eine Zielmenge (meist: Menge der reellen Zahlen) ist. Ein Beispiel ist die harmonische Folge mit den Folgengliedern 1, 1/2, 1/3, 1/4, ...
Manche Folgen haben einen Grenzwert, sog. konvergente Folgen. Wir lernen Kriterien für die Konvergenz von Folgen kennen sowie Verfahren zur Berechnung von Grenzwerten.
Wir lernen, wie man eine Funktion in der Umgebung einer Entwicklungsstelle x0 durch Polynomfunktionen mit wachsendem Grad immer besser annähern kann.
Wir betrachten auch die Reihenentwicklungen der trigonometrischen Funktionen sin x und cos x und stellen fest, dass es einen Zusammenhang gibt zwischen der komplexen Exponentialfunktion eix und den trigonometrischen Funktionen.
Wir beschreiben einstufige Übergangsprozesse (z. B. das Wechselverhalten von Kunden oder Populationsentwicklungen) mit Hilfe von linearen Gleichungssystemen, Übergangsgraphen, Tabellen und Übergangsmatrizen und wandeln die verschiedenen Darstellungen flexibel ineinander um.
Wir lernen, wie lineare Gleichungssysteme mit Hilfe von Matrizen und Vektoren dargestellt werden können, und lösen diese mit dem Gauß-Algorithmus.
Mit Matrizen kann man rechnen: Man kann sie addieren, mit einem Skalar (d. h. mit einer Zahl) multiplizieren und auch miteinander multiplizieren. Das Produkt zweier quadratischer Matrizen deuten wir im Zusammenhang mit mehrstufigen Übergangsprozessen.
Wir werden untersuchen, inwieweit die bekannten Rechengesetze (Kommutativgesetz und Assoziativgesetz) auch für die Matrizenmultiplikation zutreffen, und bestimmen von invertierbaren Matrizen das Inverse und deuten dieses im Zusammenhang mit Übergangsprozessen.
Die wiederholte Multiplikation einer Matrix mit sich selbst stellt eine Potenz dieser Matrix dar. Daraus können sich in Sachzusammenhängen interessante Folgerungen ergeben.
Für Übergangsprozesse mit absorbierenden Zuständen (z. B. bei Glücksspielen) bestimmen wir Absorptionswahrscheinlichkeiten sowohl näherungsweise durch mehrfache Hintereinanderausführung als auch exakt durch das Lösen des entsprechenden Gleichungssystems.
In diesem Modul geht es darum, den mathematischen Hintergrund von asymmetrischen Verschlüsselungsverfahren kennenzulernen und zu verstehen.
Wir lernen hierzu den Euklidischen Algorithmus zur Bestimmung des größten gemeinsamen Teilers zweier Zahlen (ggT) kennen sowie den erweiterten Euklidischen Algorithmus und wenden beide Algorithmen an Beispielen an.
Wir beschäftigen uns mit modularer Arithmetik, um unter anderem die Werte von Potenzen modulo n, insbesondere im Fall großer Exponenten, effizient berechnen zu können.
Wir lernen den Satz von Euler kennen und beweisen ihn mit Hilfe der zuvor erarbeiteten Kenntnisse. Daraus ergibt sich dann der kleine Satz von Fermat.
Dieser Satz ist die mathematische Grundlage des RSA-Verfahrens, des ersten veröffentlichten asymmetrischen Verschlüsselungsverfahrens. Wir verschlüsseln damit Nachrichten und machen plausibel, dass die zugehörige Entschlüsselung wieder die ursprüngliche Nachricht ergibt.
Demnäscht vielleicht mehr hierzu...
Siehe auch: Lehrplan für den Mathe-Vertiefungskurs (PDF-Datei, ca. 57 kB)